Após resolver o Exercício de Programação do Bhaskara, fica aquela dúvida: como saber se o exercício está certo? Quais valores eu coloco para \(a\), \(b\) e \(c\) de forma que eu saiba qual o resultado que deve ser mostrado?
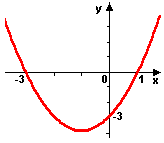
Uma forma de fazer isso é esboçarmos uma parábola e recorrermos a alguns cálculos simples que aprendemos no 2º grau. Vamos ver um exemplo? Observe a parábola abaixo:
Primeira observação: os pontos onde o gráfico cruza o eixo \(x\) são as raízes (por definição). Ou seja, depois que colocarmos os valores de \(a\), \(b\) e \(c\), que ainda não sabemos quais são, no nosso programa, ele deve indicar os valores \(-3\) e \(1\).
Segunda observação: o ponto onde o gráfico cruza o eixo \(y\) é o coeficiente \(c\). Ou seja, já sabemos que \(c=-3\) e, agora, só precisamos descobrir os coeficientes \(a\) e \(b\)!
Mas, como fazer isso? Oras, aprendemos lá no 2º grau que:
- A soma das raízes deve dar \(\frac{-b}{a}\)
- O produto das raízes deve dar \(\frac{c}{a}\)
Assim, no nosso exemplo, a soma das raízes é \(-3+1=-2\) e o produto é \(-3\cdot 1=-3\). Primeiro, calculamos o valor de \(a\) usando o produto (equação 2) porque já sabemos o valor de \(c\): \(\frac{c}{a}=produto \Rightarrow \frac{c}{a}=-3 \Rightarrow \frac{-3}{a}=-3 \Rightarrow a=\frac{-3}{-3} \Rightarrow a=1\).
Agora que já sabemos o valor de \(a\) e \(c\), podemos calcular \(b\) usando a soma (equação 1): \(\frac{-b}{a}=soma \Rightarrow \frac{-b}{a}=-2 \Rightarrow \frac{-b}{1}=-2 \Rightarrow -b=-2\cdot1 \Rightarrow -b=-2 \Rightarrow b=2\).
Pronto! Agora, ao rodarmos nosso programa para cálculo das raízes de uma equação de 2º grau, se entrarmos com os valores \(a=1\),\(b=2\) e\(c=-3\), a saída deve ser \(x_1=-3\) e \(x_2=1\).
Proposta
Escreva um algoritmo que lê os os pontos onde uma parábola intercepta o eixo \(x\) (as raízes) e o ponto onde ela intercepta o eixo \(y\) (o coeficiente \(c\)) e que mostra os coeficientes \(a\), \(b\) e \(c\) de uma equação de 2º grau que gera essa parábola.
Solução: GitHub