Olá! No artigo anterior, vimos o que são algoritmos, quais as formas de representá-los e quais suas características. Também começamos a entender o que é lógica de programação e quais as fases que todo algoritmo possui. Além disso, comentei que o próximo passo seria aprendermos uma linguagem de programação que, para quem está começando, seria o Portugol. Mas, antes de darmos prosseguimento nisso, gostaria de deixar as minhas respostas para as perguntas que deixei lá! Achou que ficariam no limbo? 😉 Vou aproveitar a deixa para aprofundar na questão das fases dos algoritmos e em mais alguns conceitos. Vamos lá?
Os Algoritmos da Maria
A primeira pergunta que havia deixado era: “Reveja o trecho do diário da Maria e procure pelas palavras em itálico. Você consegue criar um fluxograma para cada um dos algoritmos dos quais elas fazem parte?”. Procurando pelas frases que contêm essas palavras, chegamos aos seguintes casos:
Mudei o percurso que costumo fazer de carro pois fiquei sabendo que estava congestionado.
Antes de criarmos o fluxograma, vamos pensar um pouquinho? Quais as informações que a Maria precisou para tomar a decisão de mudar o percurso? Seria a situação do trânsito, certo? Essas informações necessárias para dar prosseguimento à tarefa que queremos realizar é o que chamamos de entrada do algoritmo. E, após ela saber dessa situação, ela resolveu fazer um percurso diferente do que ela costuma fazer. O percurso escolhido é o resultado do algoritmo. É o que chamamos de saída do algoritmo. Tendo isso em visto, podemos dizer que a Maria, sabendo da situação do trânsito decidiu entre fazer um percurso habitual ou um alternativo. Essa parte que não é a entrada nem a saída, é o que chamamos de processamento. Dito tudo isso, podemos esquematizar o seguinte:
- Entrada: situação do trânsito.
- Processamento: se a situação do trânsito estiver boa, vou pelo caminho habitual; caso contrário, vou pelo caminho alternativo.
- Saída: o percurso escolhido.
Separando o problema (escolher um percurso para ir até o trabalho) nessas três partes, fica mais fácil pensarmos na solução e em chegarmos ao nosso fluxograma:
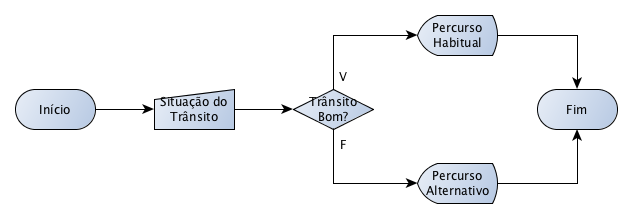
É interessante notar que temos dois comandos, instruções, ações, símbolos de saída, um para cada caso. Se você não lembra dos símbolos, reveja o artigo anterior ou baixe o e-book “O Senhor dos Algoritmos”. Mas, voltando ao ponto, seria interessante que houvesse apenas um símbolo de saída, indicando “Percurso Escolhido”. Para isso, teríamos que falar de um assunto chamado “variáveis” que iremos ver posteriormente e não fazem muito sentido no tipo de questão que estamos lidando aqui (mais sobre isso logo adiante).
Outro ponto que gostaria de comentar é que as fases de entrada e saída, nesse exemplo particular, se confundem diretamente com os comandos, instruções, ações, símbolos de entrada e saída. Uma coisa é a fase e outra é o comando. As fases podem conter, por si só, uma lógica complexa. Por exemplo: imagine que ao tentar verificar a situação do trânsito, a Maria tente ver isso pela Internet, mas ela está fora do ar. Nesse caso, ela ainda pode fazer essa verificação pelo rádio. Percebe que, nesse caso, existe uma outra lógica, um outro algoritmo, só para obter a informação de entrada?
Manobrei, manobrei e manobrei enquanto o carro não estava corretamente alinhado à vaga.
A solução desse caso pode ser encontrada no artigo anterior:

No entanto, vamos pensar nas três fases… Quais seriam elas?
- Entrada: quando pensei nessa solução, levei em conta a situação dada que é o carro não estacionado; poderíamos pensar, também, em qual vaga ela quer estacionar. Ou seja, as entradas poderiam ser: qual o carro e qual a vaga. Mas, como estão subentendidos, podemos pensar que a situação que a Maria tem nas mão é o carro não estacionado.
- Processamento: veja que a Maria tem um carro não estacionado e quer ter, como resultado, o carro estacionado. Para isso, ela deve manobrar um pouco e verificar se o carro está alinhado à vaga. Caso o carro não esteja alinhado, ela deve manobrar mais um pouco e repetir esse processo até que o carro esteja alinhado.
- Saída: nesse caso, após concluir sua tarefa, a Maria tem, como saída, como resultado, o carro estacionado.
É interessante notar que esse fluxograma tem o que chamamos de laço, loop ou repetição. Toda vez que precisamos repetir uma operação, precisamos criar um fluxo, ou seja, traçar uma flecha para algum comando que ficou para trás no fluxograma. Isso cria essa ideia de laço:

Coloco o queijo ou o presunto primeiro? Lógico, não perdi muito tempo com isso e escolhi ao acaso.
Nessa situação, a Maria queria fazer um sanduíche de pão, presunto e queijo. No entanto, ela ficou com uma dúvida: qual ingrediente ela colocaria primeiro no pão? Assim, ela escolheu ao acaso, de forma aleatória, randômica… Vamos analisar em como podemos montar um fluxograma para essa situação? Qual seria a entrada? Podemos pensar que seria o presunto e o queijo. Sim, se estivéssemos pensarmos no problema “fazer um sanduíche”. Mas, o caso aqui é bem mais específico: é qual ingrediente ela coloca primeiro. Se analisarmos de trás para frente, podemos chegar mais facilmente no fluxograma. Quais seriam as saídas possíveis? Presunto primeiro (e, queijo em segundo) ou queijo primeiro (e, presunto depois). E como ela escolheu? Ao acaso… Podemos imaginar a Maria jogando uma moeda para cima e pensando “se der cara, coloco o queijo primeiro; se der coroa, coloco o presunto”. Ou seja, para ela escolher, a informação foi o resultado de se lançar uma moeda. Ou, qualquer outra fonte ou origem desse dado ao acaso. Lembra que, quando precisamos de uma informação para continuar nossa tarefa, estamos falando de uma entrada. Conclusão: a nossa entrada é o resultado de se lançar uma moeda. Assim, podemos montar o seguinte esquema:
- Entrada: resultado do lançamento de uma moeda
- Processamento: se for cara, coloco o queijo primeiro; caso contrário, coloco o presunto.
- Saída: queijo e presunto ou presunto e queijo, conforme resultado.
E, com isso, chegamos ao nosso fluxograma:
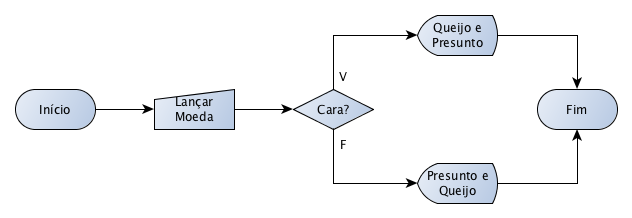
Fiquei trocando de canal até achar algo legal.
Nesse exercício, a Maria fica sapeando os canais até achar algo legal. Podemos pensar no seguinte esquema:
- Entrada: nenhuma.
- Processamento: verificar se eu gosto do canal. Se não gostar, troco de canal e verifico novamente.
- Saída: canal escolhido (com algo que eu goste).
Assim, temos o seguinte fluxograma:
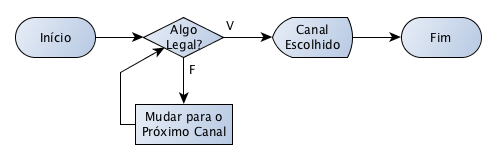
Note que, nesse fluxograma, também temos um laço, loop ou repetição. Assim, podemos levantar a seguinte questão: o que aconteceria se a Maria não achasse nenhum programa legal? Ela ia ficar trocando de canal para sempre? Sorte que os programas de um mesmo canal vão mudando com o passar das horas. Mas, poderia levar um bom tempo! Agora, se a programação não mudasse e ela não gostasse de nenhum canal, ela ia ficar num loop infinito. Isso faria com que nosso algoritmo não terminasse e, aí, não poderíamos chamá-lo assim já que não cumpriria com a característica de finitude dos algoritmos. Como podemos evitar isso? Podemos pensar na possibilidade da Maria memorizar o canal inicial e, se ela chegasse de novo nesse canal após passar pelos outros, ela ia assistir esse mesmo. Nesse caso, precisamos dessa informação, ou seja, é uma entrada:
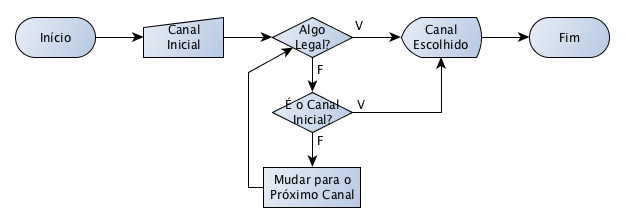
Você ainda consegue visualizar o loop?
Resolvi ler um livro enquanto o sono não chegava.
Vamos pensar um pouco nesse aqui, também. Aliás, sempre reflita um pouco no problema e em como você vai encontrar a solução! Vejamos: quando a Maria pega o livro para ler, provavelmente ele tem um marcador indicando em qual página ela parou a leitura. E, quando ela começar a sentir sono, ela vai querer marcar a página em que ela parou. Ou seja, a entrada e a saída desse algoritmo é a página do livro em que ela começou a ler e em qual ela parou, respectivamente. Podemos escrever o seguinte esquema antes de desenhar o fluxograma:
- Entrada: página inicial.
- Processamento: ler uma página do livro e verificar se está sem sono. Se sim, repete o processamento. Caso contrário, pare a leitura.
- Saída: página em que parou a leitura.
Agora, sim, podemos desenhar nosso fluxograma:
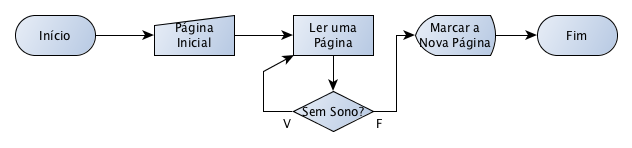
Note uma coisa interessante: neste exercício, a repetição se dá quando a condição é verdadeira. No exercício anterior, a repetição se dava quando a condição era falsa. Isso se dá pela diferença entre as palavras “enquanto” e “até”.
Mais Algoritmos
A outra pergunta que deixei foi: “Além das receitas, você conseguiria dizer outros exemplos de algoritmos descritos em linguagem natural?”
Bom, neste momento, eu consigo pensar em três:
- Descrição de uma rota de carro para ir da cidade A até a cidade B.
- Instruções para chegar, por meios dos menus, na configuração das notificações de seu celular.
- Planejamento de um roteiro de viagem.
E você? Pensou em mais alguma?
A Pastelaria da Maria
O último exercício que deixei foi: “Imagine que você foi até uma pastelaria. Tente descrever todos os passos envolvidos desde o momento em que você escolhe o seu pedido, até o momento em que você paga por ele, passando, inclusive, pelos passos que o garçom, cozinheiro e outras pessoas envolvidas têm que fazer.”
Se você parar para pensar, existem muitos, muitos passos envolvidos neste caso. O que podemos fazer aqui é usar uma técnica chamada de refinamentos sucessivos. Ela consiste em descrevemos de forma mais genérica os passos do algoritmo e, depois, refinar cada um dos passos. Por exemplo, podemos começar com a seguinte sequência para nosso algoritmo:
- Fazer pedido
- Comer o pastel
- Pagar a conta
Só que, se lembrarmos das características dos algoritmos, devemos lembrar que os passos não podem ser ambíguos (definição) e que eles devem ser básicos o suficiente (efetividade). Posso pensar que o passo 2 não está bem definido porque não sei qual é o pastel que estou comendo. E, também posso pensar que essas ações ainda não são básicas o suficiente para que possamos passar esse algoritmo para alguma outra pessoa executar (o que seria fazer o pedido?). Assim, vamos refinar cada um desses passos:
- Fazer o pedido
- Chamar o garçom
- Pedir o cardápio
- Olhar o cardápio
- Escolher o pastel que quer comer
- Pedir o pastel para o garçom
- Comer o pastel
- Pegar o pastel
- Levá-lo até a boca
- Abrir a boca
- Colocar o pastel dentro da boca
- Morder o pastel
- Puxar o pastel
- Se o pastel não acabou, voltar ao passo 2.3.
- Pagar a conta
- Chamar o garçom
- Pedir a conta
- Conferir a conta
- Paga o valor
Parece bobeira ter que descrever todos esses detalhes, mas reflita no que é a ação de comer? Provavelmente teriam mais passos ainda. Para não me estender muito, imaginei os passos acima. Dá para pensar em mais outros detalhes: e, se você quiser colocar molho de pimenta no pastel entre uma mordida e outra? E, se você quiser tomar um refrigerante? 😉
Note que ainda estão faltando passos: entre fazer o pedido e comer o pastel, teríamos a preparação do pastel e aí, nosso algoritmo poderia ficar assim:
- Fazer pedido
- Preparar o pastel
- Garçom leva o pedido até o cozinheiro
- Cozinheiro olha o pedido
- Ele separa os ingredientes
- Prepara o pastel
- Frita o pastel
- Seca o pastel no papel-toalha
- Cozinheiro chama o garçom
- Garçom leva o pastel até você
- Comer o pastel
- Pagar a conta
Mais um detalhe que poderia ser levado em conta é a forma de pagamento. Se fosse em cartão, envolveria digitar o valor na máquina, inserir o cartão, digitar a senha, retirar o cartão e retirar a impressão do comprovante. E, se fosse em dinheiro, envolveria a possibilidade de se calcular o troco se houvesse necessidade.
Quantos passos, não é mesmo? Eu tenho certeza que você vai encontrar várias possibilidade de melhoria no algoritmo acima, bem como alguns erros! 🙂 Mas, o objetivo deste exercício é mesmo usar a criatividade e você notar que os algoritmos, na vida real, envolvem muitos passos. E, quando estivermos programando em uma linguagem de programação de computadores, teremos que nos preocupar com todos os detalhes, pois é a máquina quem vai executá-lo e ela irá seguir suas instruções cegamente!!!
Algoritmos Computacionais e Não-Computacionais
Neste momento, eu espero que você tenha percebido que os algoritmos fazem parte do nosso dia-a-dia, mas nem sempre os chamamos com esse nome. Imagine que você está dirigindo e quer chegar em determinado lugar, mas está perdido. Será que você perguntaria para uma pessoa na rua dessa forma: “Por favor, você pode me ajudar? Estou precisando chegar neste lugar… Tem como me dar um algoritmo para ir até lá?”. Acho (espero) que não! 🙂
Outra coisa que você deve ter percebido é que os algoritmos estão em nossas mentes, principalmente quando estamos criando um a partir do nada. E, para que você possa explicar para alguém o que está em sua cabeça, você se expressa por meio de alguma linguagem, seja gráfica (fluxograma) ou não. De qualquer forma, você faz isso para que você ou outra pessoa possa executar seu algoritmo, ou seja, seguir suas instruções, comandos, ações.
Só que, algumas vezes queremos que um computador possa executar esse algoritmo. E aí, é necessário refletirmos: será que um computador conseguiria executar algum dos algoritmos que eu propus acima? Acredito que (ainda) não! Por isso, dizemos que eles são Algoritmos Não-Computacionais. Daqui para a frente, iremos querer tratar do outro tipo: os Algoritmos Computacionais, ou seja, os que um computador é capaz de executar. Você irá notar bem a diferença quando começarmos a ver os comandos que você pode usar para escrever seus programas (você lembra o que são programas?). Veja que esses conceitos estão ligados com o que falei no artigo anterior sobre as características fundamentais dos algoritmos, principalmente no que diz respeito à característica da efetividade. Isso é, você irá aprender um conjunto de comandos muito bem definidos e que o computador é capaz de entender e executar. Por isso, fique tranquilo! 🙂
Conclusão
Espero que a questão das fases dos algoritmos tenha ficado um pouco mais clara aqui. No decorrer do curso, iremos trabalhar mais com essas fases e veremos mais de perto situações onde cada fase pode ter uma lógica mais complicada. Mas, não se preocupe com isso agora. O que você precisa tirar de lição deste artigo é que devemos, antes de começar a escrever um algoritmo (ou programa), pensar um pouco nessas três fases.
De quebra, vimos um pouquinho sobre o método dos refinamentos sucessivos, que nos ajuda a escrevermos algoritmos complexos. (Bem) Mais para frente, veremos um conceito chamado funções (sub-algoritmos) que torna essa ideia mais clara e mais fácil de se expressar em nossos programas.
Bom, termino por aqui. Fique esperto que, no próximo artigo, iremos baixar o Portugol Studio e escrever nosso primeiro programa! Até breve!
